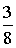分數約簡的技巧

在分數約簡中，需要很快地判斷分子、分母的最大公約數。可是當我們不能一眼看出最大公因數的時候，我們需要一步一步地將分數約到最簡單，主要的方法就是利用小的數去試一試，看是不是分子、分母的公因數。下面給出一些判斷2、3、4、5、6、9的倍數的方法：
1、2的倍數：
如果一個數是2的倍數，那么這個數一定是一個偶數。

2、3的倍數：
如果一個數的各個位數相加，所得的數是3的倍數，那么這個數是3的倍數。
例如：1236，1+2+3+6=12，12是3的倍數，所以1236是3的倍數。

3、4的倍數：
如果一個數的最后兩位數是4的倍數，那么這個數是4的倍數。
例如：124，最后兩位數是24，是4的倍數，那么124是4的倍數。

4、5的倍數：
這個是最簡單的判斷，如果一個數的最后一位數是0或者5，那么這個數是5的倍數

5、6的倍數：
當然，如果一個數既是3的倍數，又是偶數，那么一定是6的倍數。

6、9的倍數：
和3的倍數相差不遠，如果一個數的各位位數相加的和是9的倍數，那么這個數是9的倍數。

其中要提醒的是，3和9的倍數的判斷是最后用的。呵呵
當然在判斷一個數是否是3或者9的倍數的時候，可以循環利用這個規則。例如：123456789，
1+2+3+4+5+6+7+8+9=45，如果你不知道45是不是9的倍數，循環利用規則：4+5=9，那么45是9的倍數，那么就可以知道123456789是9的倍數。

分數約簡

明白分數的意義之后，分數的加法就很容易明白，3個1/8就是3/8，也就是說：

可是我們仔細看著兩個圖：

可以發現，事實上兩個圖中的黑色部分是一樣大小的，那就是說，

原因是，如果將份數增大的同時，取得的份量也增大相應的倍數，那么分數的大小并不改變。簡單說：即是說將8元分成8份取走2份和將8元分成4份取走1分，得到的錢都是2元，大小并沒有改變。得到的錢還是8元里面的
也就是說每一個分數可以寫成很多相等的分數值，但是為了記數的簡便，我們選擇分母最小的那個數來表示相等的分數，即是最簡分數：也就是分子是整數，分母是正整數，且分子和分母互質（最大公因數為1）的分數。
例如在

中我們將選擇，1/2來表示。
那么在計算結果中如果遇到不是最簡分數的時候，我們需要約簡分數。方法就是用分子分母同時除以分子、分母的
最大公約數。例如：12和15的最大公約數是3，那么：

就可以得到最簡的分數。

分數

分數是用分式（分數式）表達成

在上式之中， b 稱為分母而 a 稱為分子，可視為某件事物分成 b 份中佔 a 分，讀作「 b 分之 a 」。中間的線稱為分線。有時人們會用a/b來表示分數。

用一個圓來表示整體1，如圖：

從圖中可以看到，這個圓分成了8份，那么每一份就是

既然1份就是，那么這個圖中：

黑色的部分就是

除法 二

《 除法一》計算除法對于很多人來說都是一件很困難的事情，原因就是如何很快地確定商是什么。其實這是有一定竅門的。例如計算：

很容易知道，21小于9的倍數和20小于9的倍數相差不遠。那么在試商的時候，可以先將21看作20，那么20×3=60最接近74，于是用3試。

得到的商是3，余數是11。
同樣的道理，如果除數是兩位數的情況，
1、同時個位數是1、2、3的情況，例如21，32，41等等，這時在試商的時候可以將除數的個位數看作零，也就是說：將21看作20，32看作30，41看作40來試商。
2、如果個位數是7、8、9的情況，例如27，48，59等等，這時在試商的時候可以將除數像四舍五入的方式對待來試商，也就是說：將27看作30，將48看作50，將59看作60。
在應用這些方法的時候，同時要知道余數永遠要小于除數！

等弧對等角的證明

在一個圓周上面，相等的弧長對應的圓周角相等。這個定理在初等幾何（圓）的證明中非常重要。

如圖：

我們知道，角A=角1+角2，角5=角1+角3+角2+角4，同時角1=角3，角2=角4.
所以角5=2×角A。
對于圖：

如果A移動到A'，那么角5=角1'+角3'-（角2'+角1'）。同樣可以得到，
角5=2×角A'。
所以可以得出：等弧所對應的圓周角相等。